Okay, Color Spaces

Colors… in… spaaaaaaace

What is a “color space?”

Well first you take some colors.

• red
• yellow
• blue

And then you arrange them, however you like, into some kind of space:

The space has coordinates. In the little toy color space we've just defined, red is at $(x=0,y=1)$, yellow is at $(-1,-1)$, and blue is at $(1,-1)$. That’s a color space!

You might ask: what kind of color might we find at the origin: $(0,0)$? Right now, it’s undefined, but we could put anything there: black, gray, brown, heck – even hotpink if we wanted.

Which brings us to the first point: color spaces are all constructs. People just make them up! Useful ones are constructed in order to do useful things, but there’s no, like, One True Fundamental Color Space.

When I was a kid, various art teachers taught me about The Color Wheel with its Three Primary Colors and its Three Secondary Colors and while that wheel did help me make greenish paint when the classroom only had yellow and blue, it also gave me some wrong ideas about color.

You see, just like the food pyramid, the RYB color wheel is made up. It’s a conceptual model, invented by people, who invented it by arranging a set of things into an abstract, hierarchical geometry, as a problem-solving tool. The RYB color wheel was developed in order to give artists and eight-year-olds a (rough) way to (loosely) predict what might happen when they mixed certain pigments. But colors – like tastes, touches, and smells – don’t have any kind of innate geometric relationship to each other. When we arrange colors around a wheel, or set them into any other space: we did that.

All of this is to say: color spaces can’t really be “right” (or “wrong.”) They can only be useful.

CIE XYZ: a very useful color space

The toy color space that I constructed at the beginning of this post is useless. It doesn't help us do anything.

What might a useful color space do? Well, just like the RYB color wheel, maybe it could help us predict how different colors will mix.

And lo, in 1931, an international team of experts got together in England and laid out a color space that does exactly that¹. They used science and math. They called themselves the International Commission on Illumination (aka le Commission Internationale de l'Éclairage, aka the CIE), and they called their color space CIE XYZ.

Here are three colors plotted in CIE XYZ: a red, a green, and a blue.

The first thing you might notice is, it's 3D! Turns out, most useful color spaces have at least three dimensions, although in order to visualize various things, people will often flatten 3D spaces into 2D.

Now, CIE XYZ isn’t limited to three colors. In fact, it contains all of the colors².

So let’s fill our visualization out a bit. The red, green, and blue that that I plotted above happen to be the three primary colors that define the P3 color gamut. Here’s the rest of the P3 gamut, plotted in CIE XYZ:

Cross section $Y$

Unlike our toy color space, which defined three discrete colors, CIE XYZ is continuous. I could pick any point in the CIE XYZ space and get a unique color. That’s cool, but it’s still not useful. What’s useful about CIE XYZ is the way it helps people solve the related problems of predicting mixes and creating matches of arbitrary colors.

CIE XYZ is built out of three functions. Those functions take some wavelength of light as input, and give $X$, $Y$, and $Z$ as output. This means you can sample some real-world light with a spectrometer, do some math, and get an $X$, a $Y$, and a $Z$, which locate that light’s color within the CIE XYZ space.

Let’s say I’ve got a pair of spotlights:

• color(xyz-d65 0.40 0.25 0.05) (red)
• color(xyz-d65 0.30 0.50 0.10) (green)

What color will I see if I shine them both, full-blast, at the same spot? CIE XYZ lets me predict the result. The space has been structured in just such a way that all I have to do is add up the $X$s, $Y$s, and $Z$s:

color(xyz-d65 0.70 0.75 0.15) (yellow!)

By slicing a lil’ parallelogram out of the CIE XYZ space – with one corner at black, two corners at the locations of our two spotlights, and the last corner at the location of their full-blast mix – I can predict what any combination of these two lights, at any intensity level, is going to look like.

With a little matrix algebra, I can go the other way: CIE XYZ lets me take a color and figure out whether-and-how I can replicate it by mixing another set of colored lights. This is extremely useful! Once I know the CIE XYZ coordinates of the subpixels that make up a physical pixel on a display, I can calculate how to mix them to precisely replicate all kinds of colors. With CIE XYZ, I can dial up, say, color(xyz-d65 0.12 0.07 0.31) on wildly different displays and get consistent results.

CIE XYZ turns color mixing problems and color matching problems into math problems. This has proven so useful that every modern color space is defined in terms of CIE XYZ. When we say that a system is “color managed” what we’re saying is: it’s built on top of CIE XYZ.

So! CIE XYZ! It’s useful! But it’s not useful for everything.

Perceptual uniformity (is hard)

Predicting mixes was one thing I learned in art class. Another? Creating even gradients.

When you’re learning a new medium or technique – crosshatching, watercolors, whatever – this is the 101 lesson; it’s like playing scales in music. Practicing gradients gives you a facility with the tools and teaches you how to judge and create even intervals of color.

CIE XYZ is very bad at this. If we draw a straight line through the CIE XYZ space and mark that line at evenly-spaced intervals, sampling at each mark, we get bad gradients. Like this lopsided grayscale:

CIE XYZ hangs out in the light-gray zone forever, and then gets very dark very fast – that last step is a doozy.

All CIE XYZ transitions from lighter colors to darker colors suffer from this problem³.

Transitions between light colors and dark colors aren’t the only problem. Gradients between different hues can look lopsided, too.⁴.

My favorite perceptual problem with CIE XYZ is that transitions between blue and gray get weirdly purple in the middle:

Color nerds call color spaces that are good at creating even gradients “perceptually uniform.” Meaning, the distance between any two colors in the space corresponds to “how different” they look, to people. There are all sorts of reasons folks might want a color space like this.

• Maybe they’re making a data visualization and want to use color differences to communicate value differences.
• Maybe they’re making image-editing software, and want modifications to feel consistent and intuitive.⁵
• Maybe they’re storing colors digitally, and want to store as many perceptually-different colors in as few bits as possible.
• Maybe they’re trying to measure color contrast in order to ensure accessibility.
• Maybe they’re trying to render a nice, even-looking gradient as a design element.

For these tasks (and more!), a perceptually-uniform color space is the right tool for the job.

As discussed, CIE XYZ ain’t it.

(sRGB, the web’s dominant, default color space, was constructed in order to model a typical 1990s cathode-ray tube display; sRGB also ain’t it.⁶)

The first attempt at “it” (a perceptually-uniform color space) was made by Albert Munsell, who described his space in 1905 (charmingly, as a “COLOR TREE”) and published an “Atlas” to it in 1913.

The central “trunk” of Munsell’s TREE goes from black at the bottom, through grey in the middle, to white at the top. The middle expands outwards into a rainbow of “branches”, with each angle around the trunk representing a particular hue. Each branch starts off desaturated near the middle, and gets more and more saturated the further out it goes.

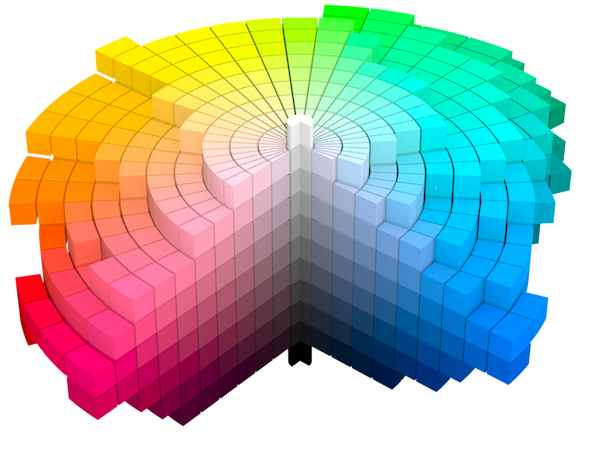
Whereas every color theorist before Albert Munsell (and many, after him) worked from the “frame in”, trying to cram all visible colors into a regular shape like a wheel or a sphere or whatever, Munsell instead worked from the “content out”, trying to create even intervals between adjacent colors and letting each “branch” extend as far as it could before he reached some limit of saturation. The resulting solid resembles a lumpy, lopsided spinning top.

Albert’s COLOR TREE was immediately recognized as useful, and is in fact still used. But as time passed, problems accumulated:

• It was based on his own personal judgements rather than scientific experiments, and it showed.
• (Just like our toy color space!) the COLOR TREE is discrete, and only specifies the positions of a few hundred individual colors.
• Those colors didn’t cover anything close to the range of colors that people can actually see.

In the decades that followed, people tried to solve all of these problems, both iterating on Munsell’s tree and creating wholly new continuous color spaces that attempted to be perceptually uniform. Arguably, the most significant of those spaces was constructed by the CIE, in 1976: CIELAB. (Ever heard of “Lab color”? This is that.)

CIELAB is a relatively simple mathematical transform of CIE XYZ, making it easy to implement in “color managed” digital contexts. But – tragically! – CIELAB isn’t exactly perceptually uniform. Worse, the more experiments people did, the clearer it became that no three-dimensional space could ever be perceptually uniform; three dimensions just cannot capture all of the weird and wonderful ways that our eyes and brains process color comparisons. As anyone who has entered a Turrell or debated The Dress can tell you, color perception is wild. When trying to predict how people are going to perceive the difference between two colors, we need to account for way more than three variables. For instance:

• How large are the color samples? Where are they in the subject’s field of vision?
• How long have they been there? What other colors were there recently?
• Crucially, what other colors surround the samples?
• What’s the ambient background lighting like?

(I’m not even going to mention the ways in which we “read” scenes within semantic and cultural contexts, which also matter.)

So, after 1976, people started developing more-and-more complicated models that attempted to account for more-and-more of this complexity. We’ve spent fifty years coming up with these things. Many of the resulting color models are considered too complex for most practical applications, and yet none of them is considered perfect.

I am fascinated that the CIE knocked predicting color mixes and matches out of the park in 1931, and yet here we are, almost a hundred years later, still trying to solve the problem of predicting color differences. Our mastery of mixing and matching makes us very good at capturing and replicating colors. But, because we can’t predict differences well, we’re still bad at automating all sorts of other color tasks, which remain as much art as science.

One thing that’s absolutely clear is that the problem of perceptual uniformity is never going to be solved with a plain-Jane three-dimensional color space. But! The entire universe of digital imaging is rooted in such spaces, because it’s all built on top of CIE XYZ.

So – what is someone who wants a perceptually-uniform space in a digital context supposed to do these days?

Oklab: it’s okay!

Until a few years ago, the best tool for these sorts of jobs was still CIELAB. So I was excited when CIELAB-for-the-web was first proposed in 2016. And then I waited for five years, until it finally shipped.

While I was waiting, in December of 2020, a guy named Björn Ottosson wrote a blog post. In it, he introduced a brand-new three-dimensional color space that he’d been working on: Oklab.

In an over-simplified nutshell, here’s how Björn came up with Oklab:

1. He picked a couple of best-in-class color models⁷.
2. After choosing a set of values representing “normal” viewing conditions, he used those models to generate a set of color comparison data.
3. He transformed CIE XYZ in a mathematically clean/easy way to approximately fit all of that color comparison data pretty well.

Et voila: Oklab. Here’s what it looks like:

Cross section $L$

Is it perfect? No, it is not. But is it mathematically and computationally simple? Yes! And does it perform better at most tasks requiring perceptual uniformity than all of the other simple, three-dimensional color spaces? Sure seems like it!

What happened next was astonishing: the web platform rapidly adopted Oklab. Oklab went from a blog post to shipping in Safari in fifteen months! Wild!

Photoshop soon followed suit.

So, Oklab: if you want perceptual ~uniformity, it’ll do.

OKLCH, because Munsell was a good API designer

What do Oklab’s $L$, $a$, and $b$ parameters actually mean?

• $L$ is lightness. This represents how light or dark a color looks. $L$ goes from zero to one.
• $a$ is “greeness-to-redness” with gray at zero. It’s theoretically unbounded but in practice it goes from around -0.4 to +0.4.
• $b$ is “blueness-to-yellowness” with gray at zero. Same-same with the practical approximate -0.4 to +0.4 range.

So, in Oklab, blueviolet is oklab(53.38% 0.1303 -0.2137): medium lightness, somewhat red, and rather blue.

Are you thinking what I'm thinking? $a$ and $b$ are weird.

Munsell’s COLOR TREE has much nicer dimensions:

• Lightness: height up the tree; black to white.
• Hue: angle around the trunk; just like the color wheels of my youth.
• Chroma: how far away from the trunk are we? Gray in the middle and more saturated the further away we get.

These three dimensions seem to express ways that our brains actually process color. When comparing one color to another on the same branch of Munsell’s COLOR TREE, it feels like only one thing has changed: chroma. Likewise when we go up and down the tree, or around it – both lightness and hue feel like independent variables. Whereas when we change, say, the $a$ of an Oklab color, it feels like we’re changing two things – both the hue and the chroma – simultaneously. It’s not easy to predict how changing $a$ or $b$ is going to look.

Thankfully – turns out! – Oklab was explicitly designed so that movement up/down, in/out, and around the $L$ axis works exactly like navigating Munsell’s COLOR TREE. Each type of movement changes just one, psychologically-independent thing: the lightness, chroma, or hue of the color. In order to navigate Oklab like this, we need to use a polar coordinate system, instead of a rectangular one. When we do, we refer to the space by another name: OKLCH⁸.

I should note that OKLCH was not the first color space to adopt Munsell’s lightness-chroma-hue “API”; even CIELAB had a polar version that worked like this, called LCH. But OKLCH does appear to be one of the best.

Both OKLCH and Oklab have their uses. Gradients in polar spaces work differently than gradients in rectangular spaces. They’re not better or worse, mind you – just different.

In a rectangular space, a gradient between two colors that lie on opposite sides of the space gets gray in the middle:

In a polar space, instead of drawing a straight line through the space to get from one color to the other, we orbit the origin, creating a half-rainbow of evenly-separated hues.

Some tasks (like measuring color difference) are simpler in rectangular spaces. But whenever we want to change the hue or chroma of a color independently – say, when we want to turn a color’s saturation up a notch, or theme and scheme with code – only a perceptually ~uniform, polar space will do. Right now, on the web: that means OKLCH.

So!

What have we learned?

• Color spaces are constructs, which arrange colors into some coordinate-based space.
• Colors don’t have any kind of innate spatial relationship to each other, but arranging them in various ways can be useful.
• CIE XYZ is an extremely useful color space, because it turns color mixing problems and color matching problems into math problems.
• All “color managed” digital imaging is based on CIE XYZ.
• Measuring how we’ll perceive the difference between two colors is a whole other kettle of fish; predicting differences remains an unsolved problem.
• Solving that problem – by constructing a model with perfect “perceptual uniformity” – is going to require more than three variables, but oops! We built all digital imaging on top of CIE XYZ, a three-dimensional space.
• Oklab tries to resolve this by making many assumptions and simplifications, in order to model everything we’ve learned about perceptual uniformity in a simple three-dimensional space.
• Oklab is pretty good!
• People tend to think about color in terms of three variables: lightness, chroma, and hue.
• Oklab does a good job of isolating these variables, but in order to use them, we have to navigate it using polar coordinates instead of rectangular ones. When we navigate Oklab this way, we call it OKLCH.

Time to play

Enough reading! Go! Explore!

• Evil Martians’ OKLCH color picker is fantastic.
• I couldn’t have written this post without Color.js. It’s doing all of the color math in the interactive visualizations, and I had multiple color notebooks open at all times, while writing.
• Speaking of the interactive illustrations, if you want to visualize other gamuts in other color spaces, the ColorAide Interactive 3D Color Space Models demo has you covered.
• For a different entry point into understanding color spaces in general and CIE XYZ in particular, check out Bartosz Ciechanowski’s Color Spaces. It’s chock full of interactives.
• I know I linked to it earlier, but Björn Ottosson’s original Oklab blog post is very good.

Okay, bye! 🌈